[Python] 프로그래머스 / Summer/Winter Coding(~2018) / 지형 편집

문제 링크

 

무식한 방법 (시간복잡도 초과)

이 문제는 상당히 쉽지 않은데, 사실 첫눈에는 쉬워보인다. 그냥 하라는 대로 하는 건 어렵지 않기 때문이다. 문제는 시간복잡도이다.

from collections import Counter

def solution(land, P, Q):
    
    sqz_land = []
    for wall in land :
        sqz_land += wall

    min_h = min(sqz_land)
    max_h = max(sqz_land)
        
    sqz_land_counter = Counter(sqz_land)
    min_cost = float('inf')

    for flattened_h in range(min_h, max_h+1) :

        cost = 0
        for h in sqz_land_counter :
            if flattened_h != h :
                if h < flattened_h :
                    cost += P*(flattened_h - h)*sqz_land_counter[h]
                if h > flattened_h :
                    cost += Q*(h - flattened_h)*sqz_land_counter[h]

        min_cost = min(min_cost, cost)

    return min_cost

 

위의 코드는 Counter 모듈과 hash 자료구조인 dictionary를 사용하여 제법 시간복잡도 최적화가 잘 된 코드이다. 그럼에도 불구하고 

 

미분의 활용 (정답은 아니지만 정답에 한발짝 가까워짐)

사실 보통은 미분을 활용했다고 표현하지는 않고, 패러메트릭 서치(Parametric Search)라고 부른다. 즉 이 경우에는 평탄화 높이(a)를 파라미터로 해서 그것에 대한 최적값을 구하는 것이다. 근데 그게 우리가 고등학교 시절 미분으로 풀어냈던 그런 문제들이다.

 

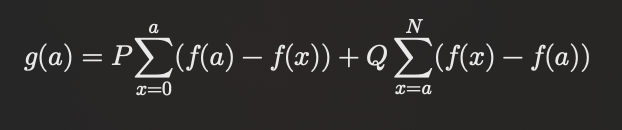
어려워하지 말고 끝까지 봐보자..

높이 x에 대해 f(x)를 높이 x에 해당하는 블록의 개수라고 정의했을 때, 높이 a로 평탄화를 진행하기 위한 cost를 g(a)로 정의하자. 그러면 우리의 목표는 g(a)의 최소값을 찾는 것이다. 

 

만약, 이 f(x)가 이산함수가 아니라 연속함수였으면, g(a)는 아래와 같이 정의될 것이다.

 

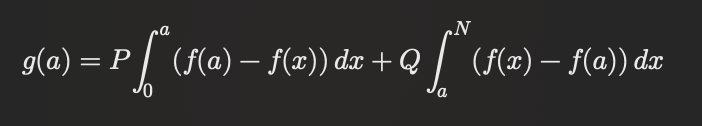
이 경우, g(a)의 최소값을 찾기 위해서는 g'(a)=0 이 되는 a를 구하면 되었던 것을 우리는 기억한다. 다만 문제는, f(x)가 이산함수이기 때문에, f'(a)를 구할 수 없다는 것이다.

 

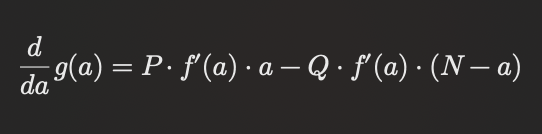
그러므로 우리는 다른 방법을 찾아야 한다. 혹시라도 수치해석이나 경사하강법(Gradient Descent)을 배운 사람이라면, 도함수값의 양수/음수 여부만 알아도 다음 탐색 범위가 좁혀진다는 것을 이해할 수 있을 것이다. f(a)와 f(a+1)을 비교하여 f'(a)를 알아낸다는 그 아이디어만을 가져와 탐색하는 것을 패러메트릭 서치(Parametric Search)라고 한다. 이를 이용한 코드는 아래와 같다.

from collections import Counter, defaultdict

def calculate(flattened_height, counter, P, Q):
    cost = 0
    for h in counter:
        if h < flattened_height:
            cost += P * (flattened_height - h) * counter[h]
        elif h > flattened_height:
            cost += Q * (h - flattened_height) * counter[h]
    return cost

def solution(land, P, Q):
    sqz_land = []
    for wall in land:
        sqz_land += wall

    min_h = min(sqz_land)
    max_h = max(sqz_land)
    
    sqz_land_counter = Counter(sqz_land)
    cost_dict = defaultdict(int)

    while min_h < max_h:
        mid_h = (min_h + max_h) // 2

        if mid_h in cost_dict:
            cost1 = cost_dict[mid_h]
        else:
            cost1 = calculate(mid_h,     sqz_land_counter, P, Q)
            cost_dict[mid_h] = cost1

        if mid_h + 1 in cost_dict:
            cost2 = cost_dict[mid_h + 1]
        else :
            cost2 = calculate(mid_h + 1, sqz_land_counter, P, Q)
            cost_dict[mid_h+1] = cost2

        if cost1 <= cost2:
            max_h = mid_h
        else:
            min_h = mid_h + 1

    return cost_dict[min_h]

 

 

 

누적합의 접목 (정답코드)

위 코드는 거의 다 도착했었지만, 시간복잡도가 몇몇 문제에 대해서 초과된다. 위 코드의 문제점은 calculate()함수가 조금 비효율적이라는 것이다. 그래서 누적합을 이용해서 calculate() 함수를 효율화할 수 있다.

from bisect import bisect_left, bisect_right
from collections import Counter

def calculate(h, heights, cumulative_counts, cumulative_heights, P, Q) :
    idx_lower = bisect_left(heights, h)
    idx_upper = bisect_right(heights, h)

    if idx_lower > 0 :
        total_counts_lower = cumulative_counts[idx_lower - 1]
        cumulative_heights_lower = cumulative_heights[idx_lower - 1]
    else :
        total_counts_lower = 0
        cumulative_heights_lower = 0

    if idx_upper < len(cumulative_counts) :
        total_counts_higher = cumulative_counts[-1] - cumulative_counts[idx_upper - 1]
        cumulative_heights_higher = cumulative_heights[-1] - cumulative_heights[idx_upper - 1]
    else :
        total_counts_higher = 0
        cumulative_heights_higher = 0

    cost_add = P * (h * total_counts_lower - cumulative_heights_lower)
    cost_remove = Q * (cumulative_heights_higher - h * total_counts_higher)
    return cost_add + cost_remove

def solution(land, P, Q) :
    sqz_land = []
    for wall in land:
        sqz_land += wall

    sqz_land_counter = Counter(sqz_land)

    heights = sorted(sqz_land_counter.keys())
    counts = [sqz_land_counter[h] for h in heights]

    cumulative_counts = []
    cumulative_heights = []
    cum_count = 0
    cum_height = 0
    for h, c in zip(heights, counts) :
        cum_count += c
        cum_height += h * c
        cumulative_counts.append(cum_count)
        cumulative_heights.append(cum_height)

    min_h = min(heights)
    max_h = max(heights)

    cost_dict = {}

    while min_h < max_h :
        mid_h = (min_h + max_h) // 2

        if mid_h in cost_dict :
            cost1 = cost_dict[mid_h]
        else:
            cost1 = calculate(mid_h,     heights, cumulative_counts, cumulative_heights, P, Q)
            cost_dict[mid_h] = cost1

        if mid_h + 1 in cost_dict :
            cost2 = cost_dict[mid_h + 1]
        else:
            cost2 = calculate(mid_h + 1, heights, cumulative_counts, cumulative_heights, P, Q)
            cost_dict[mid_h + 1] = cost2

        if cost1 <= cost2 :
            max_h = mid_h
        else:
            min_h = mid_h + 1

    if min_h in cost_dict :
        return cost_dict[min_h]
    else:
        return calculate(min_h, heights, cumulative_counts, cumulative_heights, P, Q)