Classifier-Free Diffusion Guidance 논문 요약

Diffusion계의 필수논문이 되어버린 Classifier-free Diffusion Guidance 

 

Classifier-Guidance가 있었다.

Mode Coverage(얼마나 다양하게 만드는가)와 Sample Fidelity(얼마나 샘플과 유사하게 만드는가)는 trade-off 관계이다.

다양한 생성 결과를 원할 때도 있지만, 때때로 우리는 low-temperature 결과를 원한다.

Classifier-Guidance 등장 전까지는 low-temperature 생성 방법론이 명확하지 않았다.

• 단순히 스코어 벡터를 스케일링하거나, 아니면 샘플링 과정에서 가우시안 노이즈를 줄이는 방식은 효과적이지 않다는 것이 알려져 있다.
• 전자는 "스코어 벡터는 Diffusion이 이미지를 생성할 때, 어떤 방향으로 이미지를 변화시켜야 하는지 알려주는 벡터인데, 이 벡터의 스케일을 키우면, 모델이 더 빠르게 그 방향으로 이미지를 변화시킬 수 있지 않을까?" 라는 생각에서 착안한 것

하여튼, 그래서 Classifier-Guidance는 Diffusion의 Score Estimate와, 분류기의 확률 log값의 gradient를 결합했다.

이 과정에서 직관적으로 발생할 수 있는 문제점은, "분류기(Classifier)"를 따로 학습해야 한다는 것이다.

기존에 널려있는 pre-trained classifier는 plug-in될 수 없다. 왜냐하면 이 분류기는 "노이즈가 낀" 이미지를 분류해야 하기 때문이다.

 

이 논문에서는 정확히 이 지점에서 의문을 제기한다. 어떤 "노이즈가 낀" 이미지를 생성할 때, classifier로부터 높은 점수를 받을 수 있도록 train되는데, 이것이 적대적 공격(Adversarial Attack)과 정확히 같은 원리라는 것이다.

 

이제는 10년이 넘어버린 고전 중의 고전 논문이지만, 그래도 아래의 이미지는 꽤나 유명하다.

판다 이미지에 조금의 노이즈를 더했더니 긴팔 원숭이로 분류되는 현상, https://arxiv.org/abs/1412.6572

 

물론, 이제는 이러한 현상이 꽤나 많이 해결된 것으로 알고 있다. 하여튼, 어쨌든 이미지에 노이즈를 조금 섞어 분류기 성능을 높이도록 train하는 것은 실질적으로 분류기를 속이는 노이즈가 되도록 유도할 뿐 Diffusion의 Sample Fidelity를 높일 수는 없으리라는 것이 이 논문 저자들의 주장이다.

 

더 나아가, Classifier-Guidance는 실질적으로 GAN과 크게 다르지 않다고 지적한다.

 

Classifier-Free Guidance는 분류기를 전혀 쓰지 않는다.

그럼 Classifier-free Guidance는 어떻게 Sample Fidelity를 맞추느냐?

이들은 Conditional Diffusion Model(조건부 확산모델)과 Unconditional Diffusion Model(비조건부 확산모델)의 score를 혼합한다.

 

자세히 살펴보자.

사실 이 부분은 일반적인 Diffusion 수식과 크게 다르지 않다.

다만 DDPM에서 봤던 수식에 익숙해져 있다면, 약간 헷갈릴 수는 있다. λ<λ' 이다. 즉, λ가 작아져가는 과정이 forward process이다. 

 

 

이 부분이 내용이 좀 어려운데,

• 어쨌든 샘플링 과정은 λ값이 점진적으로 커지는 T단계를 거치는 거다.
• 이는 이산시간 ancestral sampler를 따른다는 것인데, 다시말해 각 단계마다 데이터의 확률 분포에 따라 샘플을 생성하는 것이다. 그런데 T → ∞ 이면, SDE(확률적 미분 방정식)에서 샘플을 생성하는 것과 사실상 같다. 이는 Song et al., 2021b에서 논의된 바와 같다.
  • 확률적 미분 방정식이란, 결정론적 미분 방정식에 무작위성을 추가한 것을 말한다 (예: 기하 브라운 운동 방정식)
• 그래서 p_θ(z)는 이산이 아니라 연속시간에서의 분포이다.
• 한편, 분산의 경우, tilde{σ_{λ'|λ}} 와 σ_{λ|λ'} 사이를 로그 공간에서 보간하는 방식으로 계산된다. 즉, reverse process에 적용되는 분산과 forward process 분산을 보간한다는 것.
• 이 보간에 있어 사용되는 하이퍼파라미터 v의 경우, z_λ에 의존하는 것보다, 그냥 constant로 넣는 게 더 낫다.

 

ε-prediction을 사용한다고 한다. 이는 모델이 직접적으로 데이터를 예측하는 것이 아니라, 입력 데이터에서 노이즈를 예측하는 방식이다. 그리하여 목적함수는 예측 노이즈와 실제로 추가되었던 노이즈 차이를 최소화한다. 

 

논문에서는 갑자기 확 주제가 넘어가는 감이 좀 있지만...

• 어쨌든 실험적 환경에서 "실제로" T → ∞는 불가능하다. 그러므로 우리는 각 time step λ의 분포를 고려해야 한다.
• p(λ), 즉, λ의 분포가 uniform하지 않다면 학습목표는 weighted variatioal lower bound, 즉 변분하한(ELBO)으로 해석될 수 있다(?)
• p(λ)는 cosine noise schedule에 기반하여 hyperbolic secant 분포로 설정된다.
• ε-prediction 함수 ε_θ(z_λ)는 로그밀도 함수의 기울기를 추정한다.
• 학습된 모델에서 sampling은 Langevin Diffusion(Langevin Dynamics를 확률적 샘플링에 적용한 것)에서 p(z_λ)로 샘플랑하는 것과 유사하며, 결국 원본 데이터의 분포에 수렴한다.
• 조건부 생성 모델에서는 클래스 레이블 등의 조건이 모델에 추가 입력으로 제공되어 조건부 데이터 생성을 수행한다.

 

Guidance 얘기는 아직 시작도 안 함

지금까지는 Diffusion 모델에 관한 이야기였고... 그래서 어떻게 guidance를 했는지는 이제부터 시작합니다.

 

우선 기존 Classifier-Guidance에서 쓰던 걸 보면,

 

그냥 직관적으로만 보아도, 기존 Diffusion 모델의 목표 분포인 log p(z_λ|c) 에다가, 분류기에 관한 식 log p(c|z_λ) 를 넣어놓은 것을 볼 수 있다.

 

그리하여 수정된 확률분포는 z|c와 c|z를 모두 따른다.

 

Classifier Guidance 를 적용하면, 각 클래스의 조건부 분포는 Non-Gaussian으로 변하고, 확률질량이 높은 신뢰도를 가진 방향으로 이동하게 되므로 샘플 다양성이 줄어든다.

또한 이론적으로는, unconditional 모델에 w+1 강도의 guidance를 적용하는 것은, 결과적으로 conditional 모델에 w 강도의 guidance를 적용하는 것과 다름이 없어야 한다. 그러나 실험을 막상 해보면, conditional 모델이 더 좋은 결과를 얻었다고 한다. 그 이유는 아마도 conditional 모델이 이미 클래스 정보를 반영하고 있기 때문이다.

 

이게 중요한 이유는, 곧 나오는 Classifier-Free Guidance 수식이 아마도 위 현상에 착안한 것으로 보이기 때문이다.

 

일단은 Classifier-Free Guidance의 알고리즘부터 살펴보자.

SNR은 λ랑 같다고 보면 된다.

Training을 보면, 미리 설정된 확률로 클래스 정보를 누락해서, conditional과 unconditional training이 모두 진행되는 걸 볼 수 있다.

 

그건 그건데... 이 논문을 쓰신 분들이 워낙 천재적인 분들이다보니 논문을 굉장히 축약해서 쓴 부분이 있는 것 같다.

알고리즘1에서 (x, c)는 p(x, c) 이미지 분포로부터 가져온 이미지 한 장에 해당한다. 그렇다면 이미지 한 장에 대해 forward process와 reverse process를 반복하면서 ε() 함수를 학습하려면, 4~7번 줄 알고리즘을 아래와 같이 쓰면 조금 더 정확할 것 같다:

for each image (x, c) in dataset:
    for t in range(1, T+1):  # T 시간 스텝 동안 반복
        λ_t ~ p(λ)  # 각 시간 스텝에서의 log SNR 샘플링
        ϵ_t ~ N(0, I)  # 노이즈 샘플링
        z_λ_t = α_λ_t * x + σ_λ_t * ϵ_t  # 노이즈가 섞인 데이터 생성
        # 모델이 예측한 노이즈와 실제 노이즈 간의 차이를 기반으로 학습
        gradient_step_on || ϵ_θ(z_λ_t, c) - ϵ_t ||^2

 

 

3번 줄 식은 갑자기 어떻게 나온 건지 궁금할 수도 있는데, 한번 직접 유도해보면 간단하다.

 

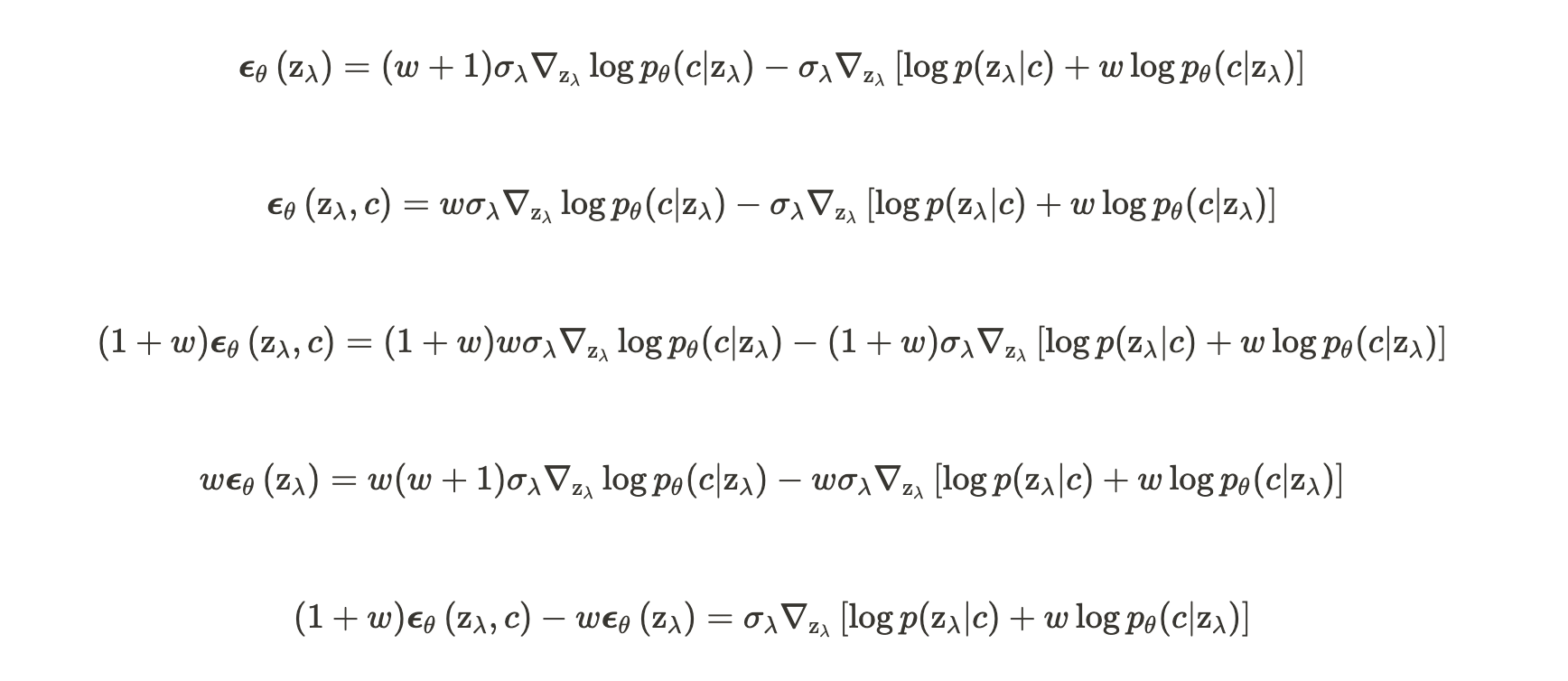
이렇게 해서, classifier가 없지만 classifier가 있는 모델이 구현될 수 있는 것이다!

솔직히 참으로 놀랍다. classifier가 전혀 없는 모델에서 c|z를 모델에 구현할 수 있다니...