CFG++: Manifold-Constrained Classifier Freeguidance For Diffusion Models 논문 리뷰

이쪽 분야에서 굉장히 유명한 랩실이다.

Abstract 읽을 때까지만 해도... "surprisingly simple fix" 보고 전혀 믿지 않았는데... 정말로 surprisinly하게 simple한 solution이었다.

 

 

1. 일단 Manifold란?

최근 Diffusion 쪽에서는 데이터 manifold에 대한 논의가 활발하다. 예를 들어 이미지 데이터가 7만 차원의 공간에 분포되어 있다고 하더라도, 실제로 분포되어 있는 걸 보면 7만차원까지 가지 않는다는 이야기이다. 심지어 어떤 연구에 의하면 데이터셋이 부족하게 훈련된 Diffusion 모델은 manifold가 0차원인 것과 다르지 않다는 (즉, 항상 같은 그림만 생성한다는) 주장도 있다. 해당 논문의 내용은 굉장히 어려워 100% 이해하기는 힘들지만, 상당히 재미있고 충격적이다.

 

조금 쉽게 비유하자면, 아마도 이론물리학 쪽의 다양한 이론에 따르면 우주공간은 적어도 4차원 이상인 것 같다. 어떤 이론은 우주가 11차원이라고 주장한다나... (진짜 잘 모름) 그럼에도 불구하고 우리 지구는 3차원 공간이다. 우리는 우리 세계가 3차원이라고 인식하고 살아도 아무런 지장이 없다. 

 

즉, 전체 분포(우주)는 초고차원이지만, 막상 인간의 분포는 3차원이듯이, 데이터 또한 전체 공간에서 작은 차원의 manifold에 분포하고 있다고 생각하면 된다.

 

2. Manifold-Constrained

Diffusion을 할 때, reverse process를 거치면서 우리는 학습 데이터의 분포 내에 있는 이미지가 생성되기를 원한다. 예를 들어 "사진" 이미지만을 학습했다면, 그 모델이 생뚱맞게 "점묘화"나 "추상화" 이미지를 생성하기를 원하지는 않는다. 그런 식으로 학습 데이터의 분포 내에서 이미지가 생성될 수 있도록 하는 것이 Manifold-Constrained의 개념이다. 

 

3. 지금은 Manifold에서 벗어남?

음, 조금은 그런 편이다. 일단 현재 conditioned diffusion의 기본이 되는 것은 CFG이다. CFG가 아닌 논문을 찾기가 더 힘든 것 같다. 당연한 게, 분류기를 별도로 만들지 않고도 분류기가 있는 효과를 낼 수 있는 똑똑한 수식을 발명해낸 위대한 논문이기 때문이다. 그런데 사실 문제점이 좀 있다. 현재 CFG는 보통 guidance scale을 지나치게 높게 설정해야 한다는 것. (5-30 정도)

 

이는 Manifold에서 벗어나게 하는 요인이 됨은 물론이요, Mode collapse, DDIM Inversion 정확도 감소 등의 문제를 일으킨다. 

이 논문은 기존의 CFG에 작은 변화를 주어 이를 똑똑하게 해결했다고 주장한다.

 

논문의 수식을 따라가보며 이를 이해해보자.

 

수식 번호는 논문의 수식 번호와 맞추었다.

 

4. 이미지 생성

 

 

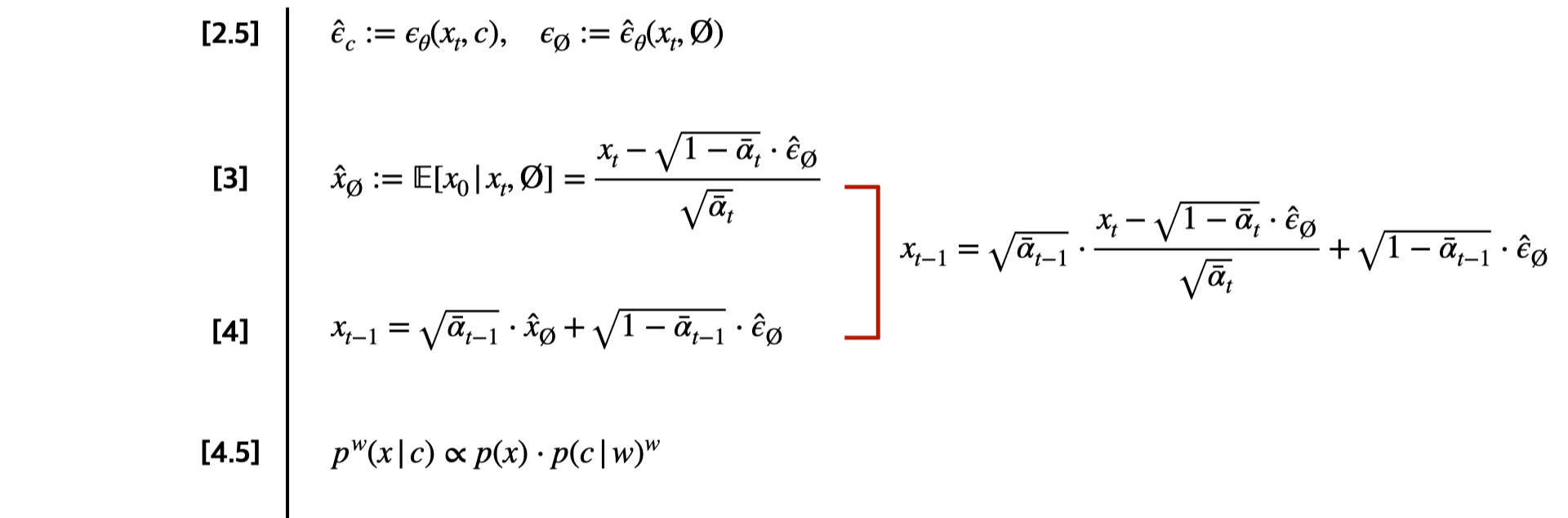
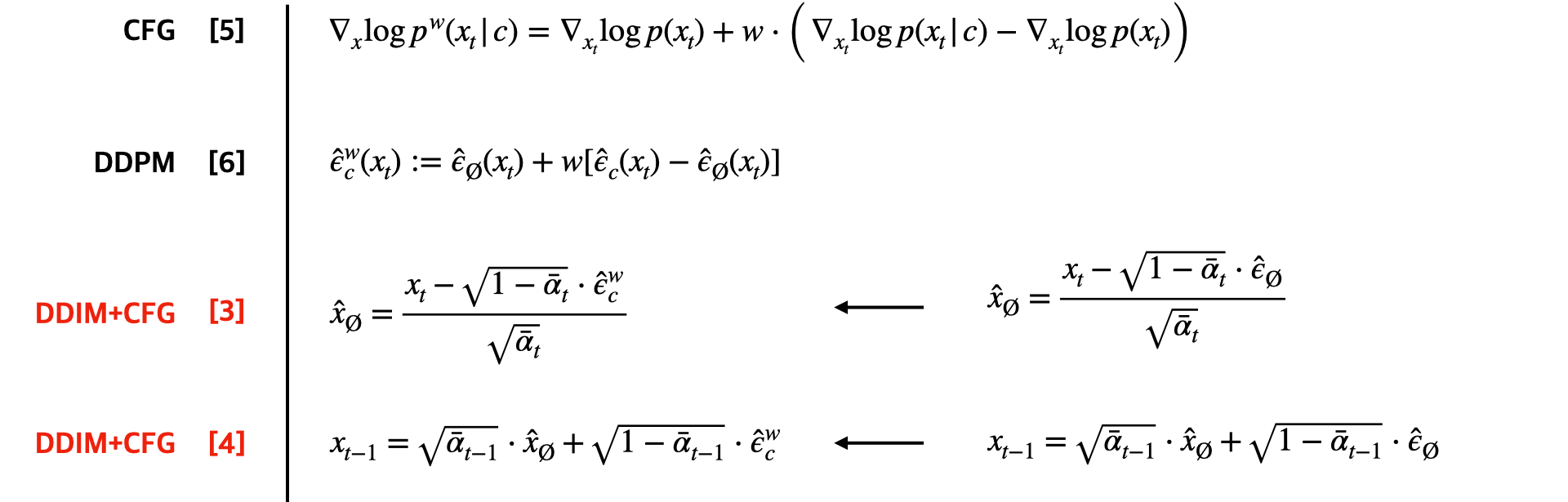
일단 여기까지는 일반적인 CFG+DDIM Sampling을 설명한 것이고, 여기서부터 CFG++ 설명이 시작된다. 

위의 수식으로 유도된 CFG++의 알고리즘이다. 보면 사실 달라진 것이라고는, w가 λ로 바뀐 것과, 저 파란색 입실론(제거 노이즈를 의미)이 조건부에서 무조건부로 바뀌었다는 것 말고는 없다. 편의를 위해 알고리즘 1을 밑에 다시 첨부한다.

 

정말 간단하다. 물론 w가 λ로 바뀐 것은 제법 큰 변화인데, 기존 5-30 사이의 w값을 주어야 했던 것을, 이제는 0-1 사이의 guidance만으로도 가능하게 되었기 때문이다. 

 

실제로 보면, diffusion 과정에서 manifold가 유지됨을 시각화해볼 수 있다.

 

이는 guidance scale을 0-1 사이 값으로 제한하여 외삽(extrapolation)이 아닌 보간(interpolation)만이 일어나기 때문이다. (forward, reverse process 모두에 해당한다)

 

 

더 나아가, text alignment가 훨씬 우수하게 지켜지는 것을 볼 수 있다. 이는 식 9번 목적함수 loss 식에서 확인해볼 수 있듯, Loss에 직접적으로 text condition을 넣었기 때문이며, 이는 이를 간접적으로 해결한 CFG와 차별된다.

 

5. 이미지 편집

이미지 편집을 위한 DDIM Inversion도 마찬가지이다. 

 

보면 DDIM Inversion 과정에서 훨씬 적은 error로 역방향 변환을 수행할 수 있다. 이는 낮은 guidance scale을 사용해 데이터 manifold를 유지하기 때문에 기존 CFG 방식에 비해 에러 누적이 적고 복원 정확도가 높기 때문이다.

 

6. 약간의 의문점

실험을 보면, 모델로는 Pre-trained SD, SDXL, SDXL-turbo, SDXL-lightning 등의 모델을 사용하였다. 이 논문은 Manifold-constrained를 주장하는데 그렇다면 얼마나 학습 데이터셋의 distribution 내에서 새 이미지가 생성되는지 검증해야 할 것 같은데... 나의 논문 이해가 부족했는지 그에 대한 명시적인 실험결과는 없어보인다.

 

다만, 아래와 같이 고글이나, 나무의 형태가 원래는 약간 비현실적이었던 데에 반해 훨씬 더 "현실적"으로 생성되므로, "현실" distribution manifold 내에 위치해있다고 뭐 그렇게 추측해볼 수는 있지만...